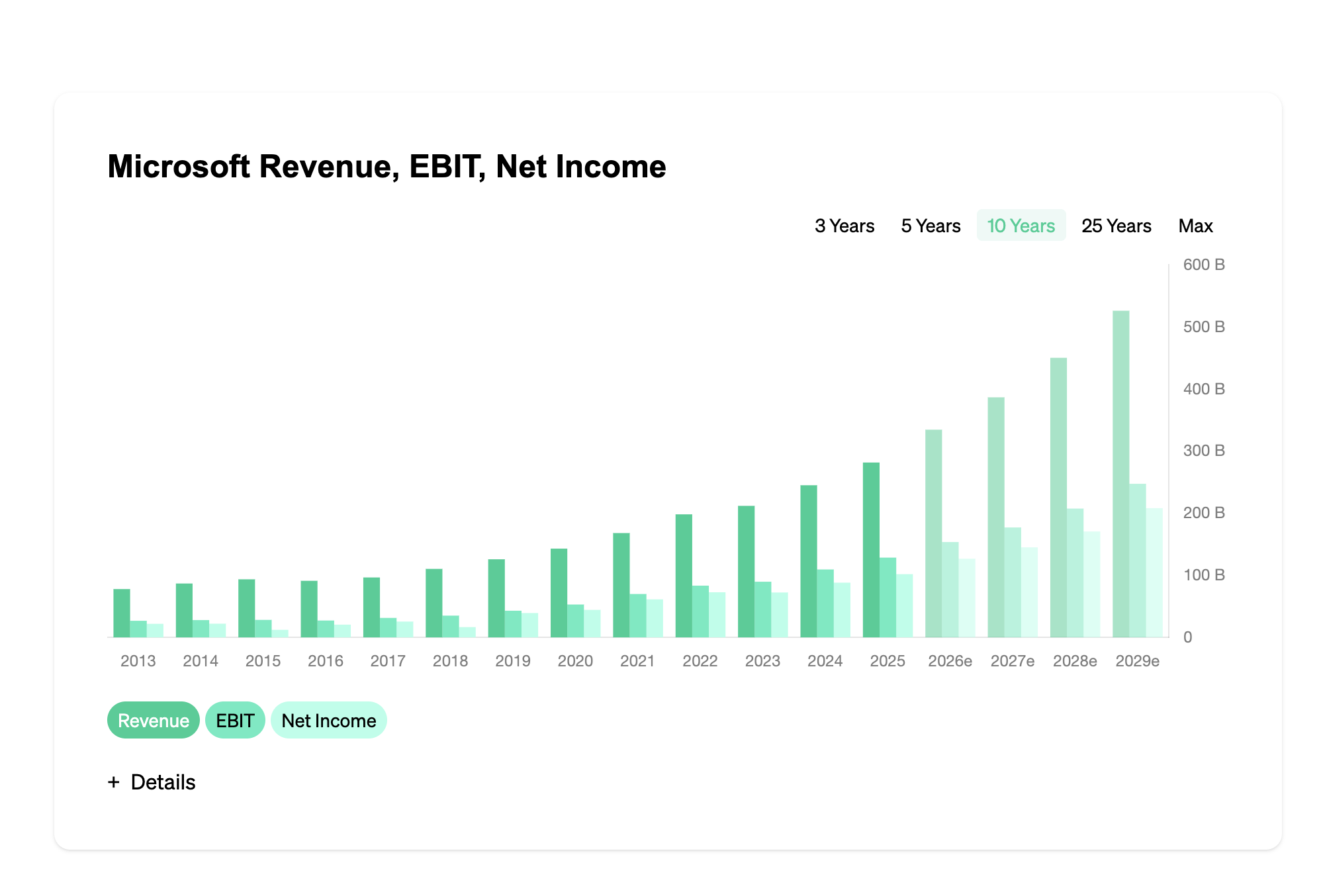
Hamiltonfunktion
Definition und Erklärung
Reconheça ações subvalorizadas com um olhar
Trusted by leading companies and financial institutions
TL;DR – Kurzdefinition
Zu den FAQs →Hamiltonfunktion: Die Hamiltonfunktion ist ein grundlegender Begriff der physikalischen Mechanik, der auch in der Finanzwelt Anwendung findet. Benannt nach dem amerikanischen Physiker und Mathematiker William Rowan Hamilton, ist die Hamiltonfunktion ein mathematisches Konzept, das die Gesamtenergie eines physikalischen Systems beschreibt. In der Finanzwelt wird die Hamiltonfunktion verwendet, um die Dynamik von Vermögenswerten wie Aktien, Anleihen, Kryptowährungen und anderen Finanzinstrumenten zu modellieren. Sie ist ein wichtiges Werkzeug bei der Berechnung von Renditen, Volatilität und anderen Kennzahlen, die für Investitionsentscheidungen von entscheidender Bedeutung sind. Die Hamiltonfunktion wird durch die Summe der kinetischen und potenziellen Energien des Systems definiert. In Bezug auf Kapitalmärkte werden dabei die kinetische Energie mit der Bewegung des Vermögenswertes und die potenzielle Energie mit den externen Kräften wie Angebot und Nachfrage oder wirtschaftlichen und politischen Faktoren in Verbindung gebracht. Ein großer Vorteil der Hamiltonfunktion ist ihre Fähigkeit, komplexe Zusammenhänge in einfachen mathematischen Formeln zu beschreiben. Durch die Verwendung verschiedener mathematischer Methoden wie partielle Ableitungen, Lagrange-Funktionen und anderen mathematischen Operationen können Investoren und Analysten Modelle entwickeln, um die Preisentwicklung von Vermögenswerten vorherzusagen und Handelsstrategien zu entwickeln. Die Anwendung der Hamiltonfunktion in der Praxis erfordert jedoch ein tieferes Verständnis der mathematischen Konzepte und der beteiligten Variablen. Erfahrung und Fachwissen sind daher unerlässlich, um die Hamiltonfunktion effektiv nutzen zu können. Insgesamt ist die Hamiltonfunktion ein wichtiges Instrument zur Modellierung und Analyse von Kapitalmärkten. Sie unterstützt Investoren und Analysten bei der Bewertung von Vermögenswerten und der Vorhersage von Markttrends. Durch die Verwendung der Hamiltonfunktion können Investoren ihre Anlagestrategien optimieren und fundierte Entscheidungen treffen.
Ausführliche Definition
Häufig gestellte Fragen zu Hamiltonfunktion
Was bedeutet Hamiltonfunktion?
Die Hamiltonfunktion ist ein grundlegender Begriff der physikalischen Mechanik, der auch in der Finanzwelt Anwendung findet. Benannt nach dem amerikanischen Physiker und Mathematiker William Rowan Hamilton, ist die Hamiltonfunktion ein mathematisches Konzept, das die Gesamtenergie eines physikalischen Systems beschreibt.
Wie wird Hamiltonfunktion beim Investieren verwendet?
„Hamiltonfunktion“ hilft dabei, Informationen einzuordnen und Entscheidungen an der Börse besser zu verstehen. Wichtig ist immer der Kontext (Branche, Marktphase, Vergleichswerte).
Woran erkenne ich Hamiltonfunktion in der Praxis?
Achte darauf, wo der Begriff in Unternehmensberichten, Kennzahlen oder Nachrichten auftaucht. In der Regel wird „Hamiltonfunktion“ genutzt, um Entwicklungen zu beschreiben oder Größen vergleichbar zu machen.
Welche typischen Fehler gibt es bei Hamiltonfunktion?
Häufige Fehler sind: falscher Vergleich (Äpfel mit Birnen), isolierte Betrachtung ohne Kontext und das Überinterpretieren einzelner Werte. Nutze „Hamiltonfunktion“ zusammen mit weiteren Kennzahlen/Infos.
Welche Begriffe sind eng verwandt mit Hamiltonfunktion?
Ähnliche Begriffe findest du weiter unten unter „Leserfavoriten“ bzw. verwandten Einträgen. Diese helfen, „Hamiltonfunktion“ besser abzugrenzen und im Gesamtbild zu verstehen.
Favoritos dos Leitores no Dicionário da Bolsa Eulerpool
Umweltgutachter
Umweltgutachter - Definition eines Kapitalmarktinvestors Umweltgutachter sind hochqualifizierte Fachleute, die auf dem Gebiet der Umweltprüfung und -bewertung in verschiedenen Bereichen des Kapitalmarkts tätig sind. Ihr Hauptaugenmerk liegt auf der Evaluierung potenzieller...
Merkposten
Merkposten - Definition und Bedeutung im Kapitalmarkt Ein Merkposten bezieht sich auf eine wesentliche Position, die von einem Investor gehalten wird. In der Regel handelt es sich dabei um eine bestimmte...
Haushaltsgerade
Haushaltsgerade - Definition und Bedeutung Die Haushaltsgerade ist ein Begriff aus der Makroökonomie und beschreibt eine lineare Gleichung, die das Gleichgewicht zwischen Einkommen und Konsum in einer Volkswirtschaft darstellt. Sie ist...
EIB
Die Europäische Investitionsbank (EIB) ist eine multilaterale Bank, die von den Mitgliedstaaten der Europäischen Union gegründet wurde. Sie wurde mit dem Ziel gegründet, Investitionsprojekte in der EU zu finanzieren und...
Dokumentenrate
Dokumentenrate – Definition, Bedeutung und Anwendung in Kapitalmärkten Die Dokumentenrate ist ein Begriff, der in den Kapitalmärkten, insbesondere im Rahmen von Kredit- und Finanztransaktionen, verwendet wird. Diese Rate bezieht sich auf...
Sparkassenbilanz
Die Sparkassenbilanz ist eine finanzielle Übersicht der Sparkassen, die als regionale öffentlich-rechtliche Institute fungieren und eine zentrale Rolle im deutschen Bankensystem spielen. Sie stellen die größte Gruppe von Kreditinstituten in...
Bundesoberbehörde
Die Bundesoberbehörde bezieht sich auf eine Behörde in Deutschland, die eine übergeordnete und zentrale Rolle in der Verwaltung von Kapitalmärkten und der Regulierung der Finanzindustrie innehat. Als eigenständige Institution wird...
Kaskadensteuer
Kaskadensteuer ist ein Konzept der deutschen Kapitalertragsbesteuerung, das die steuerliche Behandlung von Investmentfonds betrifft. Sie bezieht sich auf die Besteuerung von Erträgen, die innerhalb einer Fondsstruktur wiederholt anfallen. Diese Art...
Instandhaltungskosten
Instandhaltungskosten sind ein Begriff aus dem Bereich der Finanzanalyse und beziehen sich auf die regelmäßigen Kosten, die zur Sicherstellung der ordnungsgemäßen Funktionsfähigkeit von Vermögenswerten, insbesondere im Anlagevermögen, anfallen. Bei der...
Vertragsanbahnung beim Arbeitsverhältnis
Die Vertragsanbahnung beim Arbeitsverhältnis bezieht sich auf den rechtlichen Prozess, der vor dem Abschluss eines Arbeitsvertrags zwischen einem Arbeitgeber und einem Arbeitnehmer stattfindet. Sie umfasst alle Schritte, die Unternehmen unternehmen,...